Have you ever wondered how the musical notes we use were chosen?
I mean when I was growing up I was learning one thing in music class (do-re-me-fa-so-la-ti-do!) and another in science class (440Hz) and never the twain did meet…
So what gives? I always suspected the musical community were being scientific, but their language was all Greek to me.
Years passed and only rarely did I get the chance to wonder at this question – and meantime my science education was getting the upper hand – I learned how sounds travel through the air and how the ear works – how deep, low notes are the result of compression waves in the air, perhaps a few meters apart, while higher pitched sounds where compression waves much more tightly packed, perhaps millimeters apart. I also learned a note could have any frequency, and so no reason to pick out any ‘special’ frequencies.

However, just recently I realized, in a flash of light, that with an infinite number of notes to choose from, musicians had very deliberately selected only a few to make music with, and I suddenly wanted to know why. Was it arbitrary? Was it the same in different cultures? Why did some notes seem to go together and others seem to clash? And of course, as The Provincial Scientist, I wanted to know if our early musicians had done well in their choices.
As it is now the era of the internet I set about to find out more and thought it was so interesting, it would be a crime not to report what I learned on my blog. So here is what I learned…
In Search of Middle C
The best place to start is probably a vibrating string. The vibrating string is clearly key to pianos, harps, guitars and, of course, the entire ‘string’ section of an orchestra. If you stretch a string and pluck it, you are starting an amazing process – as you pull on the string, you create tension, you literally stretch the string and store energy in the fabric of the string. When you let go, the string shrinks under that tension, which pulls it straight. Alas, when its straight it has picked up some speed and the momentum keeps it going until the string is stretched again – thus the string swings back and forth – and it would continue forever were it not for frictional losses – energy is lost in heating the string, but some is also lost in buffeting the air around the string. The air is pushed then pushed again with each cycle creating compression waves that ripple out into the room – and into our ears. Thus we hear the string.
You can see the vibrating string doing it’s magic here:
[youtube=http://www.youtube.com/watch?NR=1&v=6JeyiM0YNo4]
You can see in the video that the string swinging back and forth is an awful lot like a wave moving up and down the string! Indeed it is!
The speed at which the wave moves (or string vibrates back and forth) – and thus the note we hear – is determined by a few simple factors – the tension in the string, and the weight of the string and the length of the string. The greater the tension, the greater the force trying to straighten the string, but the greater the weight, the more momentum there is to make it stretch out again.
It is therefore easy to get a wide range of notes from a string, start with a long, heavy wire and only tension it enough to remove all the slack. The note can then be gradually increased by decreased the length or the weight of the wire, or by increasing the tension. These are the tricks used in pianos, guitars and so on.
So far so good. But if you have several strings to tune up, what notes should you pick – from infinitely many – to make music with?
The human ear is an amazing device and can hear notes ranging anywhere from 20 to 20,000 compressions per second (the unit for per second is called Hertz or Hz for short). That is a lot of choice!
As I am sure you guessed, the key is to understand why some notes seem to ‘go together’, and the answer lies back in the vibrating string.
Overtones of Overtones
Firstly, it turns out that when you pluck a string, you actually get more than one note. While the string may swing back and forth in one elegant sweep, it may also get shorter waves, with half or a third or quarter the wavelength hiding in there too. This video shows how one spring can vibrate at several speeds:
[youtube=http://www.youtube.com/watch?v=3BN5-JSsu_4&feature=related]
Although the video shows the string vibrating at one speed each time, it is actually possible for a string to carry more than one wave at a time (this amazing fact deserves its own blog posting, but we will just accept it for now).
So when a string is plucked, the string ‘finds’ ways to store the energy with vibrations – it finds a few frequencies that carry the energy well, these are called ‘resonant frequencies’, there will be several, but they will all be multiples of one low note. As these higher notes are all multiples of a single low ‘parent’ note, they also have consistent frequency relationships between one another, 3/2, 4/3, 5/4 and many many others.
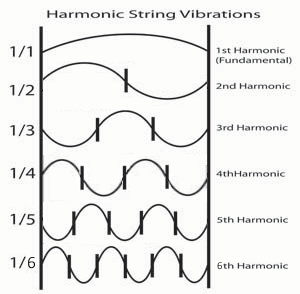
So clearly, once you have one string, and you want to add a second, you could tune the second string to try to match some of the harmonics of the first string. The best match is to pick a string whose fundamental note is at 2x the frequency of the first string. This string’s fundamental note will match the first string’s 2nd harmonic (also called its first overtone). The second string’s harmonics will also perfectly match up with pre-existing harmonics from the first string. The strings are what is called consonant, they ‘go together’.
Now although the second string will have some frequencies in common with the first string, it turns out that there is an even stronger reason why these notes will go together – it is because when you play several strings at once, you are no longer just playing the strings, the instrument you are playing is the listener’s eardrum. The eardrum will vibrate with a pattern that is some complex combination of the wave-forms coming from the two (or more) strings. When you add two notes together, it is like adding two waves together and you get an interference pattern – the interference may create a nice new sound:

If we add a low note (G1) to a note one octave higher (G2) we get a totally new sound wave.
If, as in this example, one string vibrates at exactly twice the frequency of the other, the two notes will combine to make a handsome looking new waveform, with ‘characteristics’ from both the original waves – but if the frequencies are not a neat ratio, you will get something a bit messy:
This waveform may not repeat, and is unlikely to be consonant with any other notes you may care to add.
Sometimes, when your second string is fairly close in frequency to the first (say 1.1 x the first string’s frequency) then a second phenomenon rears its head, beating. This leads to the creation of entirely new (lower) frequencies that the ear can hear [click here to listen to a sample]. The sum now looks like this:
 Beating can sound awful, though of course, the skilled musician can actually use it to create useful effects.
Beating can sound awful, though of course, the skilled musician can actually use it to create useful effects.
Beautiful Ratios
We have seen that once you have selected one note, you have already greatly reduced the ‘infinite’ choice of other notes to use with it – because only some will be consonant. Although the best consonances are at exactly 2x the first frequency, we see that once you have picked two strings, the choice for the third string is more limited. Should you be consonant first the first string or the second? Can you be consonant with both? You can be fairly consonant with both, but only by being 2x and 4x their respective frequencies. If you picked all your strings as multiples of the first string, the ‘gaps’ between the notes would be very big, akin to playing a tune with only every 12th key on a piano. So how can we fill in the gaps?
Well, early thinkers quickly realized that you can’t actually select a perfect set of notes – some combinations will mesh well, others will be just a little bit odd. This realization was probably a bitter pill for early musician-scientists to swallow.
In the end, they came up with many competing options, each designed to maximise the occurrence of good ratios – a good example is the just intonation scale:
| Note: |
C |
D |
E |
F |
G |
A |
B |
C |
| Frequency ratio to the first note: |
1 |
9/8 |
5/4 |
4/3 |
3/2 |
5/3 |
15/8 |
2 |
Here, the musician picks two notes that are consonant (C and the next C one octave higher) and then divides the gap into seven steps. Each note is a special ratio of the lower note – we get neat ratios of 5/4, 4/3 and 3/2 showing up which is good, however the ratios between adjacent notes are much less pleasing!
Aside: You will also see that the steps from B to C and E to F are rather small! Now take a look at your piano and note these notes correspond to the white keys on the keyboard that have no black keys between them! This is no coincidence…
Is the ‘just intonation’ division perfect? No, the notes are not all consonant! Remember that with 8 notes in this group, there are 7+6+5+4+3+2+1=28 ratios (or note pairs), and there is no known way to choose them to all be consonant. That is why, although most musical cultures divide their music notes into ‘octaves’ (nicely consonant frequency doublings), there have evolved many different ways to make the smaller divisions.
Western music has tended to divide the octave into 7 notes (the heptatonic scale) , you could really use any number. Let’s stick with 7 for now.
Another popular way to divide the octave is the Pythagorean tuning:
| Note: |
C |
D |
E |
F |
G |
A |
B |
C |
| Frequency ratio to the first note: |
1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/16 |
243/128 |
2 |
This scale is based on prioritizing the 3/2 overlap of harmonics and moves three notes very slightly.
It is key to remember there are dozens of ways to do this, depending on what you are trying to optimise – do you want to match the greatest number of harmonics, or some smaller number of stronger harmonics? It may even be that personal taste could come into play.
The Wonderful Piano
Have you ever wondered why you hear someone is playing something in C-minor or F-major? What is the deal there? Well, these are also ‘scales’ – alternative ways to cut up the octave, but from a specific family that lives on the piano.
You see, the piano could also divide the octave into 7 notes, and indeed it was once so divided, but with time musicians realised they could open up more subtlety in their music by adding in more notes. So they decided to add the ‘black notes’, the extra black keys on the keyboard!
So in addition to the 7 notes A,B,C,D,E,F & G, they added C#, D#, F#, G# and A# – they called them ‘half tones’ or accidentals. Of course, there are already two half steps (B-C and E-F) which is why there is no B# or E#. These extra notes gave us 12 smaller steps, and of course choosing 12 consonant notes was even harder than choosing 7!
So, after some hard thinking by scholars including J.S. Bach, a very sensible decision was made – to divide the octave into 12 ‘equal’ steps, which gives us the so-called ‘equal temperament‘, the most popular way to tune a piano. To do this, each note is 21/12 or 1.05946… times higher in frequency than the last one, such that twelve steps will eventually give you a doubling.
However, our musical notation is older than the piano and generally only allows for 7 notes per octave, so how do you write music for 12?
Despite that there are 12 notes, composers have tended to still feel some combinations of 7 notes ‘go together’ better than others and so have persisted to write music using only 7 notes, though of the many hundred’s of ways you could choose the 7 notes, they have selected 12 combinations, the 12 “Major scales“:
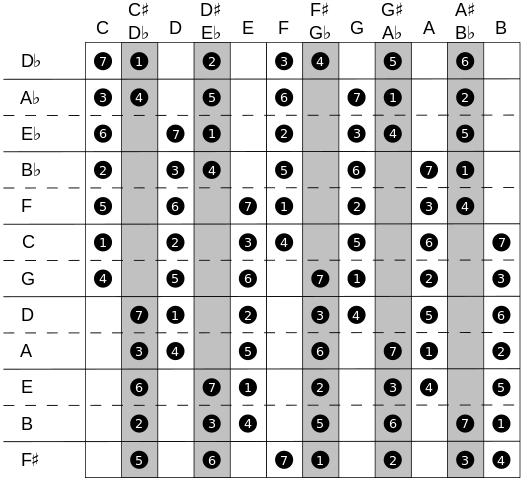
The Major Scales (down the left). Each uses only 7 of the 12 notes on the piano keyboard. The shaded vertical lines correspond to the black keys on the piano.
Personally, realising what these scales were was a breakthrough for me. Looking the above map helped me to realize several things:
- Many long pieces of music will completely ignore nearly half (5/12ths) of the keys on the piano! To play a tune based on a certain ‘scale’ is sometimes said to be played in that ‘key‘.
- The scale of C-Major ignores all the black keys, and is probably the oldest/original scale.
- Each scale is displaced 4 ‘steps’ from the previous scale (there is a #1 beneath each #5). This 1st to 5th note relationship turns out to be important.
Aside: Note that there are also the 12 “minor scales“. These scales actually use the same 12 subsets of keys as the major scales, but are ‘shifted’ – they have a different starting point (base note, or ‘tonic‘). This may seem a trivial change, but because the gaps (steps in frequency) are not all evenly sized in these scales, the major and minor scales have their two ‘small’ steps in different places, which is supposed to change the feel or mood of the music (or even the gender!)
The Number 5
The number ‘5’ in the pattern we saw above (5th note) was noticed by musicians long before me, and it shows up in other places too.
For example, we saw in the ‘just intonation’ scale above, that the note G had a frequency ratio of exactly 3/2 with the note C. This means that when you hear both together, every third vibration of the higher note will coincide with every second vibration of the lower note. They are thus highly consonant – and they are 4 steps apart on the stave. This relationship is called the ‘perfect 5th‘. It is again no coincidence that the 5th note of each scale is has a frequenxy eactly 50% higher than the 1st and is the 1st base note (aka tonic) of the next scale. Stepping in 5th’s (ratios of 3/2 in frequency) 12 times takes you through exactly 5 octaves and eventually back to the first scale.
This cycling behavior allowed the invention of a learning tool called the ‘circle of fifths‘, which helps us to understand the relationships between the scales.
Yet another aside: The ‘perfect fifth’ is called perfect if it is truly a ratio of 3/2 – but recall that pianos have their 12 notes ‘evenly spaced’ (a geometric progression) so the ratio of G to C on the C-Major scale will not be exactly 3/2 – it is actually 0.113% off!
But What About Middle-C?
Ok, so we have seen how some notes ‘go together’, and how once you have one note, you have clever ways to find families of notes that compliment that note – but that leaves just one question – how do we pick that first note?
The leading modern convention is use the note A that comes after (above) middle-C, and to set it at 440Hz exactly.
The question is, why?
Well firstly, I shall point out that the 440Hz convention is not fully accepted. For example, anyone who wants to hear, for example, the Gregorian chants the way they originally sounded, would need to use the conventions of the time. Thus there are pockets of musical tradition that do not want to change how their music has always sounded.
However, when it comes to performing a concert with many instruments, it is useful if they all adopt the same standard. The standard is thus sometimes called the concert pitch, and though 440Hz for A is common, this number has been seen to vary from 423Hz to as high as 451Hz.
So the short answer is, there is no really good reason; the choice of 440Hz really just ’emerged’ as a more common option, and when they standardized they rounded it off. While this answer is ultimately trivial, I find a little amusement in the fact that all the music we hear sounds the way it does for no particular reason!
Conclusion
Before I go, there is a video I want you to look at. I think it shows beautifully how 12 different frequency oscillations can exhibit some beautiful harmony (or harmonics!)
[youtube=http://www.youtube.com/watch?NR=1&v=7_AiV12XBbI]
All Done! Ready to Read Some Music?
The next step is to learn to read musical notation – luckily someone has already written an excellent tutorial with pretty pictures.
All I can hope is that the weird things they teach you in this tutorial will be a little less weird now we have covered the baffling origins of the notes!
Jarrod Hart (Los Olivos, CA, October 2011)
===============================
A couple more useful references:
http://www.mediacollege.com/audio/01/sound-waves.html
http://www.get-piano-lessons.com/piano-note-chart.html
http://www.thedawstudio.com/Tips/Soundwaves.html