I used to think science was the practice of the scientific method; i.e. you propose a hypothesis, you develop a test of the hypothesis, execute it and prove the hypothesis.
That worked for me until the end of high school.
At university, I was a true nerd. I read all my textbooks cover to cover (mainly because as I was too shy for girls and too poor for booze). During this time, the definition above started to fail. So much of the science was maths, statistics, observation, pattern recognition, logic and quite a bit of rote learning. Not all of it fitted into my definition of science. I became a fan of a new definition: science is the study of the nature of reality .
But then I did post-grad, and I realised that not much in science is ‘proven’ (I guess this is the point of post grad study). Evolution, for example, is not proven. That the sun revolves around the earth is not ‘proven’. I discovered that the only things that could be proven were ‘ideas’ about ‘other ideas’. Bear with me on this one.
Let us say we define the number system – this is an ‘idea’ or conceptual construction. Within this construction we can ‘prove’ that one and one is two. Because we ‘made’ the system, with rules, then we can make factual and true statements about it. We can’t do this about the real world – we cannot say anything with absolute certainly because we rely on flaky inputs like our own highly fallible perception.
It’s like that old chestnut: how can you be sure you are not living in a giant simulation? Of course you can argue that it is pretty unlikely and I would agree, and right there we have a clue to a better definition of science.
It turns out that much of modern science deals in ‘likelihood’ and ‘probability’ rather than proof and certainty. For example, we can say that the theory of evolution is very likely to be more-or-less right, as there is a lot of corroborating evidence. Science cannot be run like a law court – where the prosecution only need to reach a threshold of reasonable doubt to ‘prove’ someone guilty.
Aside for nerds: Science says you can use logic to prove things absolutely, but logic only works with ideas, and there is a breakdown between ideas and reality, so one can never prove things in reality. So it is thoroughly wrong for a court to say that someone has been proven guilty. The courts use this language as a convenience, to “draw a line under” a case as they have not found a moral way to dole out punishments based on probabilities. Imagine a world in which a murder suspect gets a 5 year sentence because the was a 20% chance he was guilty! Sports referees often operate in this decisive way, perhaps because it saves a lot of arguing!
Anyway, good science cannot just give up and say once there is consensus something passes from theory to fact. This is sloppy. We have to keep our options open – forever.
Think for example of Newton’s Laws of Motion. They are called ‘Laws’ because the scientific community had so much faith in them they passed from theory (or a proposed model) to accepted fact. But they were then found wrong. Strange that we persist in calling them laws!
It took Einstein’s courage (and open mindedness) to try out theories that dispensed with a key plank of the laws – that time was utterly inflexible and completely constant and reliable.
So it is that the canon of scientific knowledge has become a complex web of evidence and theories that attempt to ‘best fit’ the evidence.
Alas, there are still many propositions that many so-called scientists would claim are fact or at least ‘above reproach’. Evolution is attacked (rather pathetically), but the defenders would do well to take care before they call it ‘fact’. It is not fact, it is a superbly good explanation for the evidence, which has yet to fail a test of its predictions. So it is very very likely to be right, but it cannot be said to be fact.
This is not just a point of pedantry (though I am a bit of a pedant) – it is critical to keep this in mind as it is the key to improving our model.
Two great examples of models people forget are still in flux…
1) The big bang theory
2) Quantum theory
I will not go into global warming here though it is tempting. That is one where it doesn’t even matter if it is fact, because game theory tells you that either way, we better stop making CO2 urgently.
Back to the big bang.
I heard on the Skeptic’s Guide podcast today about an NSF questionnaire that quizzed people about whether they believed the universe was started with a massive explosion, and they tried to paint the picture that if you didn’t believe that, then you were ignorant of science. This annoyed me, because the big bang theory is now too often spoken of as if it were fact. Yes, the theory contributes viable explanations for red-shifted pulsars, background radiation, etc, etc, but people are quick to forget that it is an extrapolation relying on a fairly tall pile of suppositions.
I am not saying it is wrong, all I am saying is that it would be crazy to stop exploring other possibilities at this point.
You get a feeling for the sort of doubts you should have from the following thought experiment:
Imagine you are a photon born in the big bang. You have no mass, so you cannot help but travel at ‘light speed’. But being an obedient photon, you obey the contractions in the Lorentz equations to the letter, and time thus cannot pass for you. However, you are minding your own business one day when suddenly you zoom down toward planet earth and head straight into a big radiotelescope. Scientists analyse you and declare that you are background radiation dating from the big bang and that you have been travelling for over 13 billion years (they know this because they can backtrack the expansion of the universe). Only trouble is, that for you, no time has passed, so for you, the universe is still new. Who is right? What about a particle that was travelling at 0.999 x the speed of light since the big bang? For it, the universe is some other intermediate age. So how old is the universe, really?
This reminds us of the fundamental proposition of relatively – time is like a gooey compressible stretchable mess, and so is space, so the distance across the universe may be 13.5 billion light years, or it might be a micron (how it felt to the photon). It all depends on your perspective. It is much like the statement that the sun does not revolve around the earth and that it is the other way around. No! The sun does revolve a round the earth. You can see it clearly does. From our perspective at least.
Now, quantum theory.
Where do I start? String theory? Entanglement? Please.
The study of forces, particles, EM radiation and the like is the most exciting part of science. But being so complex, so mysterious, so weird and counter intuitive, it is super vulnerable to abuse.
Most people have no idea how to judge the merits of quantum theories. Physicists are so deep in there, they have little time (or desire or capability) to explain themselves. They also love the mystique.
I do not want to ingratiate myself with physicists, so I will add that the vast majority have complete integrity. They do want to understand and then share. However, I have been working in the field for long enough to know that there are weaknesses, holes and downright contradictions in the modern theory that are often underplayed. In fact these weaknesses are what make the field so attractive to people like me, but is also a dirty little secret.
The fact is that the three forces (weak nuclear, strong nuclear and magnetic) have not been explained anything like as well as gravity has (by relativity). And don’t get me started on quantum gravity.
———————-
Anyway, thinking about all these issues, I concluded that science was (definition #3) the grand (platonic) model we are building of reality, ever evolving to best fit our observations.

My man, Plato
That works well for me. However, I recently came across a totally different definition for science:
# 4) “Science is a tool to help make the subjective objective.”
OK I paraphrased it to make it more snappy. It was really a discussion about how science was developed to overcome the fallibility of the human mind. Examples of weaknesses it needs to overcome are:
- The way our perception is filtered by preconceptions
- How we see pattern where there is none
- How we select evidence to match our opinion (confirmation bias)
- How we read too much into anecdotal evidence
- etc etc.
I could go on. So ‘science’ is the collection of tricks we use to overcome our weaknesses.
I like this definition. We are all going about, and in our heads we are building our model of the world… and its time for an audit!
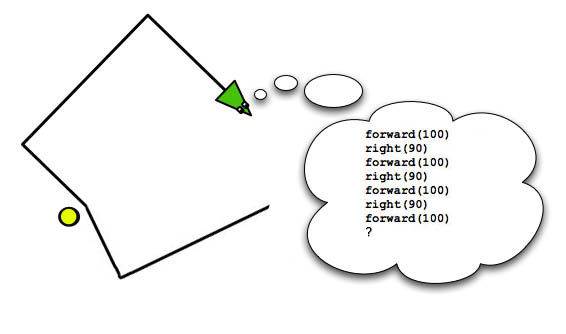 Now it turns out that it we do this, we will indeed discover an error; but why? And how do we know this?
Now it turns out that it we do this, we will indeed discover an error; but why? And how do we know this?